TOPEX/POSEIDON and TAO: Comparative simulation of two observation systems for controlling ocean circulation in the Tropical Pacific

L. Parent, J. Verron, C. E. Testut et P. Brasseur (LEGI, France)

This paper describes the results we obtained by running comparative simulations with TOPEX/POSEIDON (T/P) altimetry data and with data collected by the Tropical Atmosphere/Ocean array (TAO) to evaluate how effective they are in reconstructing surface and subsurface ocean circulation in the Tropical Pacific, using a numerical model and a data assimilation method.

Our methodology is that typically used in meteorology, based on Observing System Simulation Experiments (OSSEs). Using numerical models and data assimilation, we attempt to simulate the performance of an observation system and to optimize its configuration. The observation systems we refer to here (T/P and TAO) are already operational and do not need to be "optimized". However, we felt it would be useful to compare their performance a posteriori, under certain idealized conditions, in order to learn lessons that could benefit other observation systems and to gauge the quality of these two systems, which have made an unrivaled contribution to improving our knowledge of ocean circulation in the Tropical Pacific Ocean. There are considerable limits to this type of exercise. Until recently, these were due both to experiment strategies (based on "ideal" twin control experiments) and to the inherent limits of numerical modeling and data assimilation. But oceanography has made giant strides in recent years. As a result, we consider that our numerical ocean model and assimilation method are no longer necessarily the weakest links in the chain. The experiment strategy, however, remains an idealized one.

We used the OPA model developed by LODYC, which is based on a conventional primitive equation and includes a vertical z-coordinate. The resolution used here is 25 vertical levels, from 5 meters at the surface down to 1000 meters for the bottom layer. The meridional resolution is 1/2 at the Equator and increases with latitude, reaching 2° at the northern and southern boundaries. The zonal resolution is 1°. The full extent of the Pacific basin is considered (from 120°E to 70 W). The meridian extent of the domain is from 20 north to 20 south; a "buffer" zone between 20 and 30 links the subtropical gyres [Madec et al., 1999].

The assimilation method uses the singular evolutive extended Kalman (SEEK) filter, which is a sub-optimal reduced-order Kalman filter such that the reduced base of the error covariances evolves dynamically with the model. This method, first used by Pham et al. [1998], has already been validated for the Pacific basin [e.g., Verron et al., 1999; Gourdeau et al., 2000]. Ten empirical orthogonal functions (EOFs) are used. Observation data are assimilated every three days over a one-year period.

Experiment strategy

The underlying concept of our study is based on one simple question: How do T/P and TAO compare in terms of performance, and what happens if we decrease the density of the TAO array ? Our strategy is equally simple. We assume that data are simulated and the numerical model is perfect. The physical parameters of the observation systems and the model are therefore fully consistent.

In practice, we therefore use a time series from a free model run to extract pseudo-observations of dynamic surface topography sampled according to the real satellite ground tracks for T/P, and of sea surface and subsurface temperature at TAO moored buoy sites.

T/P and TAO observations are assimilated in comparative fashion in the same number of experiments. The reconstructed ocean fields (SSH, T, S, U, V) are compared to reference data from which observations are extracted. These data are the "absolute" reference, since all their spatial and temporal characteristics are known. Above all, results are compared "relatively", i.e., with respect to each other.
The value we use here as a basis for comparison is the root-mean-square deviation between the "reconstructed" fields derived from observations and the reference fields. The rms deviation varies quite significantly throughout the experiment. To simplify presentation, the figures below show consolidated values that correspond to the error mean over the entire one-year series. The relative error at a particular variable value (for example, the zonal velocity field at a depth of 100 meters) is represented by the annual mean of rms differences between the values of that variable over time and the reference field. A single value therefore describes how effective the observation system configuration is in controlling such a variable at this depth.

T/P scenario

T/P observations are simulated to reproduce the real satellite in terms of spatial and temporal sampling. The error on altimetric observations is assumed to be 6 centimeters rms.

TAO scenarios

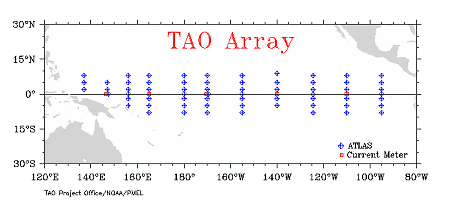
Several scenarios were considered for the TAO array. The array’s total spatial coverage was progressively degraded, as shown in Figure 1. The scenarios we tested were:

- TAO-TOT: Total coverage - TAO-Z5: Coverage degraded by removing the two outermost rows of zonal buoys, i.e., 8° N and 8° S. Five zonal lines were therefore retained: 0°, 2°N/S, and 5°N/S. - TAO-Z3: Only three zonal rows retained: 0° and 2°N/S - TAO-Z1: Only the equatorial row retained. - TAO-M: Meridian sub-sample in which one in every two meridian rows is removed. - TAO-Ouest: Only TAO buoys at 180° and westward of this longitude retained. - TAO-Est: Only TAO buoys at 180° and eastward of this longitude retained.

Temperature observations by TAO buoys are assumed to have an rms error of 0.15°C.

Figure 1 : TAO array in the Tropical Pacific.

Results

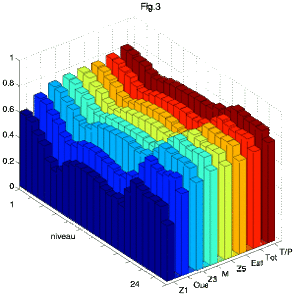
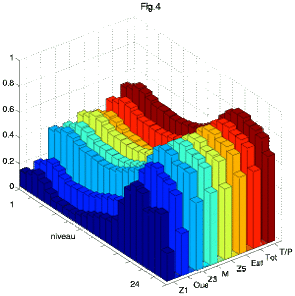
Our results are summarized in figures 2, 3, and 4. For each observation scenario and each variable (obviously, only surface values are taken into account for surface topography), performance is plotted against depth. Here we show results achieved for dynamic surface topography and globally averaged 3-D temperature and velocity fields (Figure 2), for temperature at each level (Figure 3) and zonal velocity at each level (Figure 4).

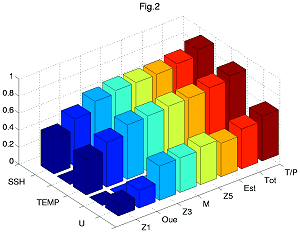
Figure 2: Performance for SSH, global temperature (T), and global velocity (U) for each scenario

Figure 3: Performance for temperature (T) as a function of depth for each scenario.

Figure 4: Performance for zonal velocity (U) as a function of depth for each scenario

Conclusions and limits

Our overall conclusion is that the T/P observation system (focusing on the Tropical Pacific) and the TAO array (comprising all 70 buoys and restricting our analysis to temperature values) offer very similar performance for controlling the model variables. This result was not at all obvious at the outset, since variables and sampling conditions are quite different.
Degrading coverage of the TAO array immediately has a big impact on performance. However, it is interesting to note that the array's zonal geographic symmetry is not a crucial factor: good TAO observation density to the east allows us to achieve a very satisfactory evaluation of the whole system, including in the western region. Moreover, zonal sub-sampling (TAO-M) by removing one in every two meridian sections has relatively little effect on overall performance.

One important result concerns the vertical dimension: consistency is high between the surface and subsurface and results are not significantly degraded at lower depths. A counter-intuitive result is even obtained for the velocity field, where control is often better at lower depths than near the surface.

We should recall the limits of this experiment and, therefore, of our conclusions. A twin control experiment strategy was used, based on the assumption of perfect-quality observations and a perfect fit between the observations and the model. This is obviously only an approximation, since models still provide only a very imperfect representation of reality. The assimilation method also assumes over-favorable conditions, since the error statistics are well known. Nevertheless, we believe that this kind of experiment is useful and that modeling and assimilation tools will be a valuable aid in defining and designing future observation systems.

References:

Gourdeau L., J. Verron, T. Delcroix, A. J. Busalacchi et R. Murtugudde, 2000: Assimilation of Topex/Poseidon altimetric data in a primitive equation model of the tropical Pacific ocean, 1992-1996. J. Geophys. Res., 105 (C4), 8473-8488.
Madec, G, P. Delecluse, M. Imbard, and C. Lévy, 1999: OPA 8.1 Ocean General Circulation Model reference manual. Note du Pôle de modélisation, Institut Pierre-Simon Laplace (IPSL), France, N°XX, 91pp.
Pham, D. T., J. Verron, and M. C. Roubaud, 1998: A Singular evolutive extended Kalman filter for data assimilation in oceanography, J. Mar Syst., 16(3-4), 323-340.
Verron J., L. Gourdeau, D. T. Pham, R. Murtugudde, and A. J. Busalacchi, 1999: An extended Kalman filter to assimilate satellite altimeter data into a nonlinear numerical model of the tropical Pacific Ocean: Method and validation, J. Geophys. Res., 104, 5441-5458.