Géodésie
La Géodésie est une science qui a pour objet la forme et la taille de la Terre. L'altimétrie contribue à cette discipline en calculant la Surface Moyenne Océanique, laquelle inclue le géoïde, c'est-à-dire le niveau de la mer en l'absence de forces perturbatrices (marées, vents, courants ...) ainsi que la dynamique moyenne des océans (courants stables). Le géoïde reflète le champ de gravité de la Terre. Ses ondulations, dont les variations de hauteurs avoisinent les +/- 100 m sur des distances de plusieurs milliers de kilomètres, sont engendrées par la distribution hétérogène des masses à l'intérieur de la croûte, du manteau ou du noyau terrestres. Les autres plus petites irrégularités de hauteurs sont également visibles sur des distances plus faibles. Ces dernières reflètent la topographie sous-marine.
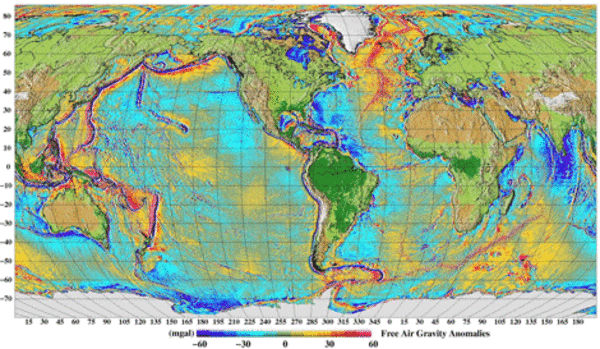
La Surface Moyenne Océanique représente le niveau de la mer dû aux phénomènes constants, calculée à partir de 16 années de données altimétriques acquises avec les missions Topex-Poseidon, ERS1&2, Envisat, GFO et Jason-1. Cette Surface Moyenne Océanique est la résultante de deux phénomènes essentiels : les courants océaniques permanents et surtout, le champ de gravité terrestre. Cette deuxième contribution, appelée géoïde, reflète les différences dans la composition interne de la Terre (zones de magma plus ou moins chaudes par exemple) et peut engendrer des variations du niveau de la mer de plusieurs centaines de mètres sur plusieurs milliers de kilomètres. A plus petite échelle (quelques kilomètres), on peut aussi observer sur cette surface (illuminée artificiellement ici pour les rendre plus visibles) les irrégularités du fond océanique qui provoquent des variations de quelques mètres à la surface (voir la page sur la bathymétrie). Plus d'information et accès aux données. (Crédits CNES/CLS 2012).
Le géoïde est défini comme une surface équipotentielle du champ de gravité de la Terre. En d'autres termes et de façon plus imagée, si nous pouvions placer des balles sur toute la surface des océans, aucune ne se verrait glisser du sommet des ondulations de cette surface parce qu'elles seraient toutes situées au même niveau, à la même gravité et, par conséquent, les eaux formant les courants ne pourraient pas couler en raison des variations de hauteurs du géoïde. Cette surface équipotentielle diffère d'environ +/- 100 m par rapport à l'ellipsoïde de référence, la forme idéale (mathématique) de la Terre.
Sur les océans, le géoïde coïncide avec une surface des océans au repos (c'est à dire sans force externe appliquée, ni vent, ni marées, et sans effet de la rotation de la Terre). Ainsi, une bosse sur le géoïde, par exemple un relief sous-marin correspond à un excès de masse, tandis qu'une fosse océanique, qu'on peut associer à un déficit de masse, va créer une dépression. Ces excès ou déficits peuvent correspondre aux reliefs sous-marins, mais aussi être liés à des variations dans le manteau terrestre. En mesurant très précisément, les ondulations de la surface des océans, les satellites altimétriques permettent de cartographier le géoïde.
Les monts et fosses au fond des océans sont la cause de très faibles variations du champ de gravité terrestre. Par exemple, la présence d'une montagne massive sur le fond océanique, qui correspond donc à un excès de masse crée une bosse localement à la surface de l'océan; ainsi, une montagne sous-marine de 1000 m de haut crée une bosse d'environ 10 cm de haut à la surface sur un rayon de 10-20 km (très approximativement, la densité de la montagne jouant également un rôle, entre autres). Cette bosse ne peut être vue à l'oeil nu, parce que sa pente à la surface des océans est très faible. Les données altimétriques, collectées à bord de plusieurs satellites altimétriques depuis plusieurs années, sont combinées pour rassembler un grand nombre de mesures, de façon à faire la moyenne des facteurs perturbateurs de la surface océanique comme les vagues, le vent, les marées et la variabilité océanique. La seule autre composante de la surface moyenne océanique qui ne soit pas le géoïde est représentée par les courants statiques (topographie moyenne dynamique) qui doit être expliquée à l'aide de différentes méthodes (voir Principe de l'Altimétrie, Circulation océanique à grande échelle).
Les ondulations du géoïde à grande longueur d'ondes
Les hauteurs de géoïde les plus importantes et les plus visibles sur une carte, correspondent à des variations de densité profondes.
Pour visualiser le géoide en 3 dimensions, voir l'interface 3D.
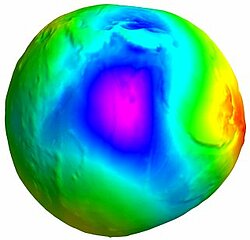
Anomalies de gravité à partir du modèle de géoïde DNSC05 (Crédits Danish National Space Center).
Références :
- Green, C. M., Fairhead, J. D., and Maus, S., Satellite-derived gravity: Where we are and what's next: The Leading Edge, 17, 77-79, 1998.
- Haxby, W. F., Karner, G. D., LaBrecque, J. L., and Weissel, J. K., Digital images of combined oceanic and continental data sets and their use in tectonic studies: EOS, 64, 995-1004, 1983.
- Li, Xiong, and Hans-Jürgen Götzez, Tutorial: Ellipsoid, geoid, gravity, geodesy, and geophysics, Geophysics, vol. 66, no. 6 (november-december 2001); p. 1660-1668, 2001.
- Sandwell,D.T., and Smith,W.H.F., Marine gravity anomaly from Geosat and ERS-1 satellites: J. Geophys. Res., 102, 10039-10054, 1997.
- Yale, M. M., Sandwell, D. T., and Herring, A. T., What are the limitations of satellite altimetry ? The Leading Edge, 17, 73-76, 1998.
Plus d'information :
- Les ondulations du géoïde sur Google Earth (Téléchargez le fichier kml et ouvrez-le dans Google Earth).
- G. Louis et al., OST/ST 2008 meeting, Modeling the oceanic gravity field by a high resolution altimetric satellite mission, pdf, (en anglais).
- Tapley, B.D. and M.C. Kim, Applications to geodesy, Satellite altimetry and Earth sciences, L.L. Fu and A. Cazenave Ed., Academic Press, 2001.
- Interface 3D interactive pour voir la Terre sous de multiples facettes.
- Images du mois sur le sujet de la géodésie :
- Ocean ridges, décembre 2002,
- Doris measures plate motion, Juillet 2002,
- Ocean circulation with gravity, Mai 2004.
- Newsletters sur le sujet de la géodésie :
- #6 : An oceanographic estimate of the geoid height in the North Atlantic (P. Le Grand, 1998),
- #6 : Application of Precise Altimetry to the Study of the Earth's Gravity Field in the Western Pacific Region and the Dynamics of the Earth (Y. Fukuda, 1998),
- #6 : Topex/Poseidon, Gravity, and the Earth's Rotation: Investigating Mechanisms and Effects of Sea Level Change (R. S. Gross, 1998),
- #6 : Monitoring geoidal potential on the basis of TOPEX/POSEIDON altimeter data (M. Bursa, 1998),
- #8 : Ocean Circulation, Height Systems and Gravity Field Studies based on Jason-1 Altimetry (E.J.O. Schrama, 2001),
- #8 : Gravity, Bathymetry, and Mesoscale Ocean Circulation from Altimetry (S.T. Gille,2001).